División de Dos Cifras: Un Viaje al Mundo de los Números: Divisiones De Dos Cifras【Ejemplos Y Ejercicios】 – Pequetareas
Divisiones De Dos Cifras【Ejemplos Y Ejercicios】 – Pequetareas – Aprender a dividir entre dos cifras puede parecer un desafío al principio, como escalar una montaña empinada. Pero, con la estrategia correcta y un poco de práctica, ¡llegarás a la cima! La división de dos cifras es una habilidad fundamental en matemáticas, un pilar que nos ayuda a resolver problemas en diversas áreas de la vida, desde calcular el costo por persona en una cena con amigos hasta distribuir equitativamente recursos en un proyecto.
Introducción a las Divisiones de Dos Cifras
La división de dos cifras, en esencia, es el proceso de dividir un número (el dividendo) en partes iguales usando otro número de dos dígitos (el divisor). Imaginemos que tenemos 126 dulces y queremos repartirlos equitativamente entre 12 amigos. Aquí, 126 es el dividendo, y 12 es el divisor. El resultado de la división, que representa la cantidad de dulces que recibe cada amigo, es el cociente.
Puede que sobren algunos dulces; esa cantidad se conoce como el resto.
Comprender las divisiones de dos cifras es crucial para avanzar en áreas como álgebra, geometría y cálculo. Nos permite resolver problemas más complejos y desarrollar un pensamiento lógico-matemático más sólido. En la vida diaria, se utiliza para calcular promedios, dividir costos, determinar cantidades proporcionales, entre otras aplicaciones.
Método Tradicional de la División de Dos Cifras
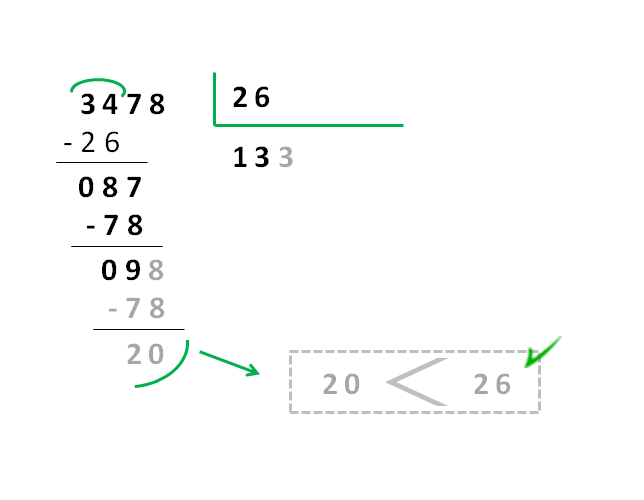
El método tradicional, o división larga, es un proceso paso a paso que nos guía a través de la división. Se basa en la estimación, la multiplicación y la resta. Es como construir una casa ladrillo a ladrillo, donde cada paso nos acerca a la solución final.
| Dividendo | Divisor | Cociente | Resto |
|---|---|---|---|
| 144 | 12 | 12 | 0 |
| 258 | 17 | 15 | 3 |
| 385 | 25 | 15 | 10 |
Por ejemplo, para dividir 258 entre 17, comenzamos estimando cuántas veces cabe 17 en 25 (una vez). Multiplicamos 17 por 1 (17), lo restamos de 25 (obteniendo 8), bajamos el 8, formando 88. Luego estimamos cuántas veces cabe 17 en 88 (cinco veces). Multiplicamos 17 por 5 (85), lo restamos de 88 (obteniendo 3). El cociente es 15 y el resto es 3.
Métodos Alternativos para la División de Dos Cifras, Divisiones De Dos Cifras【Ejemplos Y Ejercicios】 – Pequetareas
Si bien el método tradicional es efectivo, existen métodos alternativos que pueden facilitar la comprensión, especialmente para principiantes. Estos métodos a menudo se basan en la descomposición de los números o en la estimación. Es como tener diferentes rutas para llegar al mismo destino.
Un método alternativo es la descomposición del dividendo. Por ejemplo, para dividir 385 entre 25, podemos descomponer 385 en 250 +
135. Luego, dividimos cada parte por 25: 250/25 = 10 y 135/25 = 5 con un resto de 10. Sumando los cocientes (10 + 5 = 15), obtenemos el cociente total. El resto es 10.
- Descomponer el dividendo en múltiplos del divisor.
- Dividir cada parte por el divisor.
- Sumar los cocientes parciales para obtener el cociente final.
Comparando con el método tradicional, este método puede ser más intuitivo para algunos, aunque puede ser menos eficiente para números grandes.
Ejercicios de Práctica de Divisiones de Dos Cifras
La práctica es clave para dominar las divisiones de dos cifras. A continuación, se presentan algunos ejercicios para poner a prueba tus habilidades.
| Ejercicio | Solución |
|---|---|
| 486 ÷ 18 | 27 |
| 729 ÷ 27 | 27 |
| 952 ÷ 32 | 29 con resto 24 |
| 1275 ÷ 45 | 28 con resto 15 |
| 1536 ÷ 64 | 24 |
Cada ejercicio se resuelve aplicando los pasos del método tradicional, o bien, utilizando la descomposición del dividendo según se considere más adecuado.
Estrategias para Resolver Divisiones de Dos Cifras con Dificultad
Algunas dificultades comunes incluyen la estimación incorrecta del cociente o la dificultad para realizar las restas. Para superar estas dificultades, podemos usar la descomposición del dividendo, la multiplicación por aproximación o el uso de material concreto como bloques base diez para visualizar el proceso.
Por ejemplo, si tenemos dificultades con 952 ÷ 32, podemos descomponer 952 en 640 + 312. 640 ÷ 32 = 20 y 312 ÷ 32 = 9 con resto 24. Sumando 20 + 9 obtenemos 29, con un resto de 24. Visualizar esto con bloques base diez facilita la comprensión del proceso.
Aplicaciones de las Divisiones de Dos Cifras en la Vida Real
Las divisiones de dos cifras son herramientas esenciales para resolver problemas cotidianos. Desde repartir equitativamente la cuenta de un restaurante entre varias personas hasta calcular la velocidad promedio de un viaje, las aplicaciones son innumerables.
Por ejemplo, si 3 amigos comparten una pizza de 12 rebanadas, la división 12 ÷ 3 = 4 nos indica que cada uno recibe 4 rebanadas. O si un coche recorre 288 kilómetros en 12 horas, la división 288 ÷ 12 = 24 nos da la velocidad promedio de 24 km/h.
Así que, ya hemos recorrido el camino de las divisiones de dos cifras, desde los fundamentos hasta la aplicación en situaciones de la vida real. Hemos visto que, aunque al principio pueda parecer un desafío, con práctica y la aplicación de estrategias adecuadas, dominar la división de dos cifras se convierte en una herramienta poderosa e indispensable. Recuerda que la clave está en la práctica y la comprensión del proceso, no en la memorización mecánica.
Así que, ¡anímate a practicar los ejercicios, explora los métodos alternativos y aplica tus nuevos conocimientos en la vida diaria! ¡Conviértete en un maestro de la división y desvela los secretos de los números!
¿Qué pasa si el resto es mayor que el divisor?
Si el resto es mayor que el divisor, significa que el cociente es incorrecto. Debes revisar los cálculos y ajustar el cociente.
¿Existen calculadoras que ayuden con divisiones de dos cifras?
Sí, existen muchas calculadoras, tanto físicas como online, que pueden realizar divisiones de cualquier tipo, incluyendo las de dos cifras. Sin embargo, comprender el proceso manual es fundamental para desarrollar el razonamiento matemático.
¿Es importante saber el método tradicional si existen métodos alternativos?
Si bien los métodos alternativos son útiles, comprender el método tradicional proporciona una base sólida y ayuda a entender el funcionamiento de la división a un nivel más profundo.
